Yves Meyer e Ingrid Daubechies trabajaron, en la década de los 80, en el desarrollo de la moderna teoría matemática de las ondículas. Podemos imaginar estos objetos abstractos como átomos que, convenientemente unidos, representan los sonidos y las imágenes, de un modo que permite comprimirlos sin casi pérdida de calidad o eliminar el ruido que ha aparecido durante su obtención.
Las ondículas se emplean en multitud de escenarios, uno de ellos es el procesado de imágenes médicas. Por ejemplo, para comprimir (y así guardar o enviar de forma eficiente) imágenes de capas cerebrales, sin perder información relevante. Lo más importante de estas imágenes son los bordes que delimitan las distintas zonas, y las ondículas permiten detectarlos de manera eficiente, guardar ésta información y desechar el resto. El resultado es una imagen de mucho menor tamaño, pero visualmente similar a la original.
Diseñar esta versátil herramienta matemática no fue sencillo. En 1984 Ives Meyer, inspirado por investigaciones realizadas sobre prospecciones petrolíferas, y empleando su profundo conocimiento del análisis armónico, ideó las primeras ondículas, no especialmente aptas para el procesamiento de imágenes. Tres años más tarde, en colaboración con Stéphane Mallat (Collège de France), creó el análisis multirresolución (AMR), una herramienta matemática basada en principios ópticos, que permite construir ondículas a partir de una partícula aún más elemental. Esta técnica fue la usada por Ingrid Daubechies en 1988 para diseñar las ondículas con soporte compacto, una de cuyas variantes es la base del algoritmo estándar de compresión de imágenes digitales, llamado JPEG2000.
Diversos tipos de waveletes también se usan para eliminar el ruido que se puede producir al escuchar un sonido, y han sido clave en la detección de las ondas gravitacionales producidas por la colisión de dos agujeros negros lograda recientemente con el experimento LIGO, entre muchas otras aplicaciones.
Por otro lado, ya a comienzos del siglo XXI, Terence Tao y Emmanuel Candès colaboraron en la creación de la técnica de percepción comprimida (compressed sensing, en inglés), que posibilita la reconstrucción de una imagen con pocas mediciones. Esto permite, entre otras aplicaciones, reducir el tiempo que se tarda en realizar un escáner sin perder la calidad de la imagen obtenida.
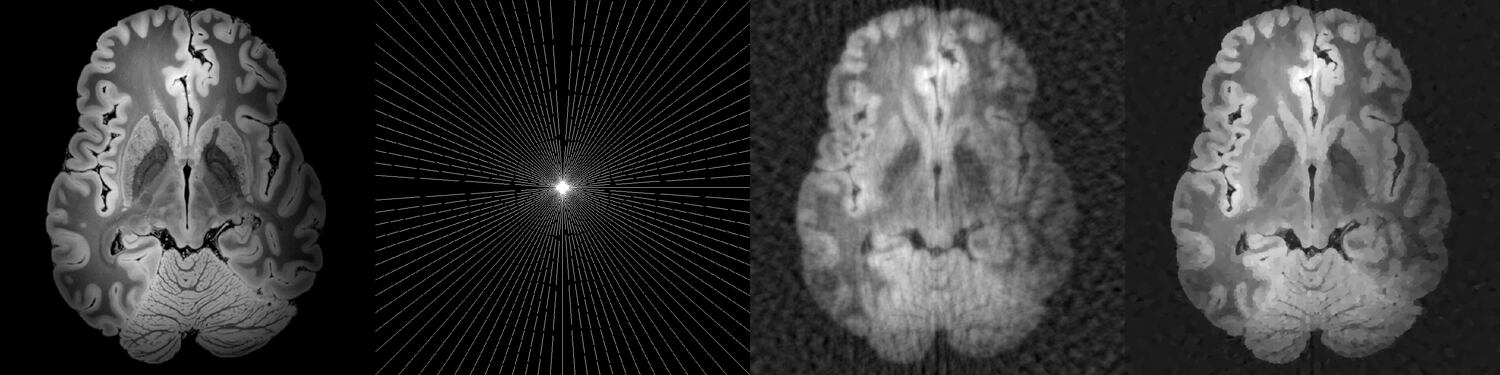
Para obtener imágenes médicas de calidad con mediciones efectuadas con resonancia magnética (MRI) es necesario efectuar muchas medidas, cambiando la dirección del campo magnético, mientras que el paciente debería de permanecer inmóvil. Esto, en la práctica, limita el número de mediciones, lo que provoca que la información disponible sea insuficiente para poder reconstruir adecuadamente la imagen deseada con la teoría clásica del análisis de Fourier. Es como si quisiéramos averiguar cuánto ha pagado cada comensal de una misma mesa conociendo solo el total de la cuenta.
Es aquí donde entra la percepción comprimida, que permite encontrar soluciones tanto a este como a muchos otros problemas indeterminados de reconstrucción de datos. La idea de Candès y Tao se basa en el principio de buscar, entre todas las soluciones posibles, la menos compleja. Su contribución fundamental fue encontrar las dos condiciones que permiten garantizar que esta solución casi siempre se acerca mucho a la correcta. La primera condición es que los datos sean dispersos. Esto significa que existe algún diccionario que permite representarlos con pocas palabras. En el caso de las imágenes, esto equivaldría a la compresión dada por las ondículas. La segunda es que las mediciones, estén lo menor relacionadas posible con este diccionario. Además, Candés y Tao fueron capaces de definir cómo tienen que ser estas mediciones ¡sin conocer el diccionario!
Todos estos trabajos, reconocidos ahora por uno de los premios científicos de más prestigio en nuestro país, muestran la importancia de las matemáticas en el desarrollo de procesos que son básicos en la tecnología actual.
Fuente: El Pais
No hay comentarios.:
Publicar un comentario